Scales and Angular Measurement
The apparent sizes of and distances between objects are described with angular measurement. This is important because the objects in the sky are often at greatly differing distances. For example, the Sun is 400 times larger than the moon. It is also 400 times more distant, so it appears to be the same size as the full moon; that is, it has the same angular size.
The system of angular measurement used by astronomers is based on divisions of the circle. The circle is divided into 360 degrees. Degrees are divided into 60 minutes of arc, or arc minutes, and each minute is divided into 60 arc seconds.
The Sun and the moon have angular diameters of about half a degree, as would a 4-inch diameter orange at a distance of 38 feet. People with keen eyesight can distinguish objects that are about an arc minute in diameter, equivalent to distinguishing between two objects the size of a penny at a distance of 70 meters (226 feet). Modern telescopes allow astronomers to routinely distinguish objects one arc second in diameter, and less. Chandra can distinguish objects down to about 0.5 arc seconds in diameter, and the Hubble Space Telescope can distinguish objects as small as 0.1 arc seconds. For comparison, 1 arc second is the apparent size of a penny seen at a distance of 4 km (2.5 miles)!
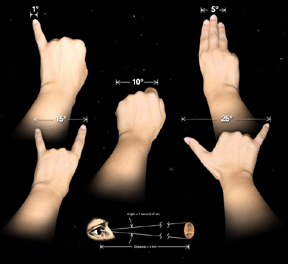
The accompanying illustration shows how you can use your hand to make rough estimates of angular sizes. At arm’s length, your little finger is about 1 degree across, your fist is about 10 degrees across, etc.
The angular diameter is proportional to the actual diameter divided by its distance. If any two of these quantities are known, the third can be determined.
For example if an object is observed to have an apparent diameter of 1 arc second and is known to be at a distance of 5000 light years, it can be determined that the actual diameter is .02 light years.
See also: Scale and Distance